tl;dr: Writeups for crypto challenges of HITCON CTF qual. The specific tags are Algebraic Immunity Attack, Fast Correlation Attack, Matrix Trace, ZKP of Factoring.
Enjoyed the game a lot though I spent one day on the wrong direction of the zkp of factoring challenge. I only solved first two challenges but I will also post the writeup of other challenges.
Broken Share
I implemented another secret sharing this year, but it doesn’t recover the flag correctly. Can you help me fix it and recover the flag? Attachment
Writeup
The challenge implements a secret sharing scheme with parameters $(n,t,p) = (48, 24, 65537)$ in python. We are given 48 shares i.e. points on the polynomial of degree 23. By lagrange interpolation, we can recover the polynomial coefficients. However, since the default type of numpy array is int64, the points evaluation may result in overflow of numpy.int64.
Denote $f(x) = \sum_{i=0}^{23} a_i x^i$ and $q, p = 2^{64}, 65537$, the point coordinate $(x_i, y_i)$ are equivalent to the following expression:
\[\begin{aligned} f(x_i) &= \sum_{j=0}^{23} a_j x_i^j \bmod q \\ y_i &= f(x_i) \bmod p \\ &= f(x_i) + k_i p \end{aligned}\]The key observation is that the first modulo operation is performed as balanced modular reduction. For an arbitrary unsigned 64-bit number $x$
- If the symbol bit of $x$ is $1$ : the
int64value of $x$ is $x - 2^{63} \cdot 2$ - If the symbol bit of $x$ is $0$ : the
int64value of $x$ is $x$
When it comes to lattice reduction, whether the modulo operation is balanced or unbalanced is of no consequence since the target small vector will not be affected by the number of moduli being subtracted. We can construct lattice from:
\[\begin{aligned} \sum_{j=0}^{23} a_j x_i^j = k_i p + y_i \mod q \\ \implies (\sum_{j=0}^{23} a_j x_i^j) p^{-1} = k_i + y_i p^{-1} \mod q \end{aligned}\]where $k_i, {a_j, j=0,\cdots,23}$ are all small values compared to the large modulus $q$.
I did not realized it during the game, so I applied a foolish lattice to solve this challenge and wasted a lot time in finding a vector of second-best brevity
Exploit
exp.py
from sage.modules.free_module_integer import IntegerLattice
import numpy as np
from Crypto.Cipher import AES
from hashlib import sha256
from random import SystemRandom
import sys
from sage.all import GF, PolynomialRing, Zmod, matrix, QQ, ZZ, block_matrix, zero_matrix, vector
from copy import copy
# https://github.com/rkm0959/Inequality_Solving_with_CVP
def Babai_CVP(mat, target):
M = mat.LLL()
G = M.gram_schmidt()[0]
diff = target
for i in reversed(range(G.nrows())):
diff -= M[i] * ((diff * G[i]) / (G[i] * G[i])).round()
return target - diff
def solve(M, lbounds, ubounds, weight=None):
mat, lb, ub = copy(M), copy(lbounds), copy(ubounds)
num_var = mat.nrows()
num_ineq = mat.ncols()
max_element = 0
for i in range(num_var):
for j in range(num_ineq):
max_element = max(max_element, abs(mat[i, j]))
if weight == None:
weight = num_ineq * max_element
# sanity checker
if len(lb) != num_ineq:
print("Fail: len(lb) != num_ineq")
return
if len(ub) != num_ineq:
print("Fail: len(ub) != num_ineq")
return
for i in range(num_ineq):
if lb[i] > ub[i]:
print("Fail: lb[i] > ub[i] at index", i)
return
# heuristic for number of solutions
DET = 0
if num_var == num_ineq:
DET = abs(mat.det())
num_sol = 1
for i in range(num_ineq):
num_sol *= (ub[i] - lb[i])
if DET == 0:
print("Zero Determinant")
else:
num_sol //= DET
# + 1 added in for the sake of not making it zero...
print("Expected Number of Solutions : ", num_sol + 1)
# scaling process begins
max_diff = max([ub[i] - lb[i] for i in range(num_ineq)])
applied_weights = []
for i in range(num_ineq):
ineq_weight = weight if lb[i] == ub[i] else max_diff // (ub[i] - lb[i])
applied_weights.append(ineq_weight)
for j in range(num_var):
mat[j, i] *= ineq_weight
lb[i] *= ineq_weight
ub[i] *= ineq_weight
# Solve CVP
target = vector([(lb[i] + ub[i]) // 2 for i in range(num_ineq)])
result = Babai_CVP(mat, target)
for i in range(num_ineq):
if (lb[i] <= result[i] <= ub[i]) == False:
print("Fail : inequality does not hold after solving")
break
# recover x
fin = None
if DET != 0:
mat = mat.transpose()
fin = mat.solve_right(result)
# recover your result
return result, applied_weights, fin
def recover(ct: bytes, poly: list, t: int):
poly = np.array(poly)
f = lambda x: int(np.polyval(poly, x) % p)
ks = [f(x) for x in range(t)]
key = sha256(repr(ks).encode()).digest()
cipher = AES.new(key, AES.MODE_CTR, nonce=ct[:8])
return cipher.decrypt(ct[8:])
n = 48
t = 24
ct = b'\xa4\x17#U\x9d[2Sg\xb9\x99B\xe8p\x8b\x0b\x14\xf0\x04\xde\x88\xb9\xf6\xceM/\xea\xbf\x15\x99\xd7\xaf\x8c\xa1t\xa4%~c%\xd2\x1dNl\xbaF\x92\xae(\xca\xf8$+\xebd;^\xb8\xb3`\xf0\xed\x8a\x9do'
shares = [(18565, 15475), (4050, 20443), (7053, 28908), (46320, 10236), (12604, 25691), (34890, 55908), (20396, 47463), (16840, 10456), (29951, 4074), (43326, 55872), (15136, 21784), (42111, 55432), (32311, 30534), (28577, 18600), (35425, 34192), (38838, 6433), (40776, 31807), (29826, 36077), (39458, 24811), (32328, 28111), (38079, 11245), (36995, 27991), (26261, 59236), (42176, 20756),
(11071, 50313), (31327, 7724), (14212, 45911), (22884, 22299), (18878, 50951), (23510, 24001), (61462, 57669), (46222, 34450), (29, 5836), (50316, 15548), (24558, 15321), (9571, 19074), (11188, 44856), (36698, 40296), (6125, 33078), (42862, 49258), (22439, 56745), (37914, 56174), (53950, 16717), (17342, 59992), (48528, 39826), (59647, 57687), (30823, 36629), (65052, 7106)]
p = 65537
mod = 2**64
pinv = int(pow(p, -1, mod))
pinv_div_2 = ZZ(pinv) / ZZ(2)
n_point = len(shares)
degree = t
mat11 = matrix(ZZ, degree + 1, n_point)
bound = mod // p
for i in range(n_point):
x, y = shares[i]
for j in range(degree):
mat11[j, i] = int(pow(x, j, mod) * pinv % mod)
mat11[degree, i] = int(-(y) * pinv % mod)
mat12 = matrix.identity(ZZ, degree + 1)
mat13 = zero_matrix(ZZ, degree + 1, n_point)
mat21 = matrix.identity(ZZ, n_point) * mod
mat22 = zero_matrix(ZZ, n_point, degree + 1)
mat23 = zero_matrix(ZZ, n_point, n_point)
mat31 = matrix.identity(ZZ, n_point) * -pinv
mat32 = zero_matrix(ZZ, n_point, degree + 1)
mat33 = matrix.identity(ZZ, n_point, n_point)
M = block_matrix(ZZ, [[mat11, mat12, mat13],
[mat21, mat22, mat23],
[mat31, mat32, mat33]])
mod = 2**64
p = 65537
bound = mod // p
lb = [0] * n_point + [0] * degree + [1] + [0] * n_point
ub = [bound] * n_point + [p] * degree + [1] + [1] * n_point
# solve CVP
res, weights, fin = solve(M, lb, ub)
print(res)
rcoeffs = [res[i]//weights[i] for i in range(n_point, n_point + degree)]
print(rcoeffs)
poly = rcoeffs[::-1]
print(recover(ct, poly, t))
Hyper512
I don’t know how to design a secure stream cipher, but a large key space should be sufficient to block most attacks right? Attachment
LFSR filter function
In this challenge, the four 128-bit LFSR generators are combined in a strange hash function:
def bit(self):
x = self.lfsr1() ^ self.lfsr1() ^ self.lfsr1()
y = self.lfsr2()
z = self.lfsr3() ^ self.lfsr3() ^ self.lfsr3() ^ self.lfsr3()
w = self.lfsr4() ^ self.lfsr4()
return (
sha256(str((3 * x + 1 * y + 4 * z + 2 * w + 3142)).encode()).digest()[0] & 1
)
Since $x, y, z, w$ are linear combinations of their initial state, for the sake of conciseness, they are denoted as :
\[\begin{aligned} x & = \sum_{i=1}^{128} a_i x_i \quad y = \sum_{i=1}^{128} b_i y_i \\ z & = \sum_{i=1}^{128} c_i z_i \quad w = \sum_{i=1}^{128} d_i w_i \\ \end{aligned}\]where the summation operation is defined over the field $\mathbb{F}_2$.
Then we should find a filter function $f: (x,y,z,w) \mapsto u$ i.e. $\mathbb{F}_2{}^4 \mapsto \mathbb{F}_2$ which can be computed as a boolean function from its truth table. Here are the codes computing the filter function in sage :
from sage.crypto.boolean_function import BooleanFunction
from hashlib import sha256
truth_table = []
for w in range(2):
for z in range(2):
for y in range(2):
for x in range(2):
bit = sha256(str((3 * x + 1 * y + 4 * z + 2 * w + 3142)).encode()).digest()[0] & 1
truth_table.append(bit)
f = BooleanFunction(truth_table)
fp = f.algebraic_normal_form()
print(fp)
for x in range(2):
for y in range(2):
for z in range(2):
for w in range(2):
bit = sha256(str((3 * x + 1 * y + 4 * z + 2 * w + 3142)).encode()).digest()[0] & 1
assert bit == fp(x,y,z,w)
print("yep")
Finally, the output bit is:
\[f(x,y,z,w) = xyz + xyw + xzw + yw + y + z\]It’s multivariate function of degree 3. Solving non-linear multivariate equations is NP-hard in a general sense. For this challenge, there are 2 solutions:
- Algebraic immunity and annihilator attack. (Used in my exploit)
- Fast correlation attack. (The intended solution, maple’s exploit)
I will introduce the algebraic immunity attack and you can refer to maple’s writeup for the second solution which is much faster than mine.
Algebraic Immunity Attack
Algebraic immunity is a measure of the resistance of a Boolean function against algebraic attacks. It is defined as the minimum degree of a non-zero Boolean function (or polynomial) that, when multiplied with the given Boolean function (or its complement), results in zero.
In other words, for a Boolean function $f$, its algebraic immunity is the smallest degree $d$ such that there exists a non-zero Boolean function $g$ of degree $d$ where
\[fg = 0\]The boolean function $g$ is called annihilator which means zeroing factor.
The core idea of this attack is to use the annihilator $g$ to linearize the equations if the degree of $g$ is relatively small. Observe that:
- Case 1 : the output bit of $f$ is 0 : the output bit of $g$ is uncertain.
- Case 2 : the output bit of $f$ is 1 : the output bit of $g$ is 0.
Therefore:
- If the algebraic immunity of $f$ is 1, it means $g$ is linear and we can directly build linear equations based on bits of case 2.
- If the algebraic immunity of $f$ is 2, we can build linear equations based on $\displaystyle n + \binom{n}{2}$ monomials of degree no more than 2 (XL attack).
- If the algebraic immunity of $f$ is greater than 2, it depends on the number of monomials you have. If n is too large, it may needs a lot of output bits and build a huge matrix.
For this challenge, compute $f$’s annihilator:
imu , g = f.algebraic_immunity(annihilator = True)
print(f"{imu = }, {g = }")
assert f*g == 0
The result is: \(g = yz + y + z + 1\)
Bingo! A nice annihilator of degree 2. Let’s estimate how many monomials $g(x,y,z,w) = g(x_1, \cdots, x_{128}, \cdots, w_{128})$ may generate:
\[g = (\sum_{i=1}^{128} b_i y_i)( \sum_{i=1}^{128} c_i z_i ) + \sum_{i=1}^{128} b_i y_i + \sum_{i=1}^{128} c_i z_i + 1\]There are at most $128 \cdot 128 + 128 + 128 = 16640$ monomials and the challenge provides $2^{12} \cdot 8 = 32768$ output bits. We can formulate approximately $16384$ equations from the 1s of output bits. By guessing several bits such as $y_1, z_1, z_2$, the left monomials are less than the equations and can be solved by linearization attack.
Exploit
solve_yz.sage
import os
import json
import signal
from sage.crypto.boolean_function import BooleanFunction
from itertools import combinations
from tqdm import tqdm
import secrets
from chall import Cipher, LFSR, Cipher256
MASK1 = int(0x6D6AC812F52A212D5A0B9F3117801FD5)
MASK2 = int(0xD736F40E0DED96B603F62CBE394FEF3D)
MASK3 = int(0xA55746EF3955B07595ABC13B9EBEED6B)
MASK4 = int(0xD670201BAC7515352A273372B2A95B23)
ct = "#"
enc_flag = "#"
ct = bytes.fromhex(ct)
enc_flag = bytes.fromhex(enc_flag)
class LFSRSymbolic:
def __init__(self, n, key, mask):
assert len(key) == n, "Error: the key must be of exactly 128 bits."
self.state = key
self.mask = mask
self.n = n
self.mask_bits = [int(b) for b in bin(self.mask)[2:].zfill(n)]
def update(self):
s = sum([self.state[i] * self.mask_bits[i] for i in range(self.n)])
self.state = [s] + self.state[:-1]
def __call__(self):
b = self.state[-1]
self.update()
return b
class CipherSymbolic:
def __init__(self, key: list):
self.lfsr1 = LFSRSymbolic(128, key[-128:], MASK1)
self.lfsr2 = LFSRSymbolic(128, key[-256:-128], MASK2)
self.lfsr3 = LFSRSymbolic(128, key[-384:-256], MASK3)
self.lfsr4 = LFSRSymbolic(128, key[-512:-384], MASK4)
def filter_polynomial(self, x0, x1, x2, x3):
# x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x3 + x1 + x2
return x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x3 + x1 + x2
def bit(self):
x,y,z,w = self.get_xyzw()
return self.filter_polynomial(x, y, z, w)
def get_xyzw(self):
x = self.lfsr1() + self.lfsr1() + self.lfsr1()
y = self.lfsr2()
z = self.lfsr3() + self.lfsr3() + self.lfsr3() + self.lfsr3()
w = self.lfsr4() + self.lfsr4()
return x,y,z,w
def get_yz(self):
y = self.lfsr2()
z = self.lfsr3() + self.lfsr3() + self.lfsr3() + self.lfsr3()
return y,z
def stream(self, n):
return [self.bit() for _ in range(n)]
def xor(self, a, b):
return [x + y for x, y in zip(a, b)]
def encrypt(self, pt: bytes):
pt_bits = [int(b) for b in bin(int.from_bytes(pt, 'big'))[2:].zfill(8 * len(pt))]
key_stream = self.stream(8 * len(pt))
return self.xor(pt_bits, key_stream)
key = secrets.randbits(512)
key_bits = [int(i) for i in bin(key)[2:].zfill(512)]
br512 = BooleanPolynomialRing(512, [f"x{i}" for i in range(512)])
key_sym = list(br512.gens())
cipher = Cipher(key)
cipher_sym = CipherSymbolic(key_sym)
pt = b"\x00" * 2**12
ct_bits = [int(b) for b in bin(int.from_bytes(ct, 'big'))[2:].zfill(8 * len(ct))]
print(ct_bits.count(1))
# check if yz_list.obj exists
if os.path.exists("./yz_list.obj.sobj"):
yz_list = load("./yz_list.obj.sobj")
else:
yz_list = []
for i in tqdm(range(len(pt) * 8)):
yz_list.append(cipher_sym.get_yz())
save(yz_list, "./yz_list.obj")
def all_monomials(x1s, x2s):
d1_monos = x1s[:] + x2s[:]
d2_monos = []
for xi in x1s:
for xj in x2s:
d2_monos.append(xi*xj)
return [1] + d1_monos + d2_monos
def fast_coef_mat(monos, polys, br_ring):
mono_to_index = {}
for i, mono in enumerate(monos):
mono_to_index[br_ring(mono)] = i
# mat = matrix(GF(2), len(polys), len(monos))
mat = [[0] * len(monos) for i in range(len(polys))]
for i, f in tqdm(list(enumerate(polys))):
for mono in f:
# mat[i,mono_to_index[mono]] = 1
mat[i][mono_to_index[mono]] = 1
return mat
eqs = []
for i, bit in enumerate(ct_bits):
if bit == 1:
eqs.append(yz_list[i][0]*yz_list[i][1] + yz_list[i][0] + yz_list[i][1] + 1)
x2s = key_sym[256:384]
x1s = key_sym[128:256]
monos = all_monomials(list(x1s)[1:], list(x2s)[2:])
print(f"[+] total equations {len(eqs)}")
print(f"[+] total monomials {len(monos)}")
for v1 in [0]:
for v2 in [0]:
for v3 in [1]:
new_eqs = []
for eq in eqs:
new_eqs.append(eq.subs({x1s[0]:v1, x2s[0]:v2, x2s[1]: v3}))
mat = fast_coef_mat(monos, new_eqs, br512)
mat = matrix(GF(2), mat)
B = vector(GF(2),[mat[j,0] for j in range(len(eqs))])
mat = mat[:, 1:]
print(f"[+] {mat.dimensions() = }, {mat.rank() = }")
try:
sol = mat.solve_right(B)
print(f"[+] solution found for x1[0] = {v1}, x2[0] = {v2}, x2[1] = {v3}")
print(f"[+] solution: {sol}")
ker = mat.right_kernel()
for v in ker.basis():
print(f"[+] kernel vector: {v}")
# break
except:
print(f"[+] no solution for x1[0] = {v1}, x2[0] = {v2}, x2[1] = {v3}")
continue
solve_xw.sage
import os
import json
import signal
from sage.crypto.boolean_function import BooleanFunction
from itertools import combinations
from tqdm import tqdm
import secrets
from chall import Cipher, LFSR, Cipher256
MASK1 = int(0x6D6AC812F52A212D5A0B9F3117801FD5)
MASK2 = int(0xD736F40E0DED96B603F62CBE394FEF3D)
MASK3 = int(0xA55746EF3955B07595ABC13B9EBEED6B)
MASK4 = int(0xD670201BAC7515352A273372B2A95B23)
ct = "#"
enc_flag = "#"
ct = bytes.fromhex(ct)
enc_flag = bytes.fromhex(enc_flag)
pt = b"\x00" * 2**12
class LFSRSymbolic:
def __init__(self, n, key, mask):
assert len(key) == n, "Error: the key must be of exactly 128 bits."
self.state = key
self.mask = mask
self.n = n
self.mask_bits = [int(b) for b in bin(self.mask)[2:].zfill(n)]
def update(self):
s = sum([self.state[i] * self.mask_bits[i] for i in range(self.n)])
self.state = [s] + self.state[:-1]
def __call__(self):
b = self.state[-1]
self.update()
return b
class CipherSymbolic:
def __init__(self, key: list):
self.lfsr1 = LFSRSymbolic(128, key[-128:], MASK1)
self.lfsr2 = LFSRSymbolic(128, key[-256:-128], MASK2)
self.lfsr3 = LFSRSymbolic(128, key[-384:-256], MASK3)
self.lfsr4 = LFSRSymbolic(128, key[-512:-384], MASK4)
def filter_polynomial(self, x0, x1, x2, x3):
# x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x3 + x1 + x2
return x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x3 + x1 + x2
def bit(self):
x,y,z,w = self.get_xyzw()
return self.filter_polynomial(x, y, z, w)
def get_xyzw(self):
x = self.lfsr1() + self.lfsr1() + self.lfsr1()
y = self.lfsr2()
z = self.lfsr3() + self.lfsr3() + self.lfsr3() + self.lfsr3()
w = self.lfsr4() + self.lfsr4()
return x,y,z,w
def get_yz(self):
y = self.lfsr2()
z = self.lfsr3() + self.lfsr3() + self.lfsr3() + self.lfsr3()
return y,z
def stream(self, n):
return [self.bit() for _ in range(n)]
def xor(self, a, b):
return [x + y for x, y in zip(a, b)]
def encrypt(self, pt: bytes):
pt_bits = [int(b) for b in bin(int.from_bytes(pt, 'big'))[2:].zfill(8 * len(pt))]
key_stream = self.stream(8 * len(pt))
return self.xor(pt_bits, key_stream)
class CipherSymbolicHalf:
def __init__(self, key: list, key2, key3):
self.lfsr1 = LFSRSymbolic(128, key[-128:], MASK1)
self.lfsr2 = LFSR(128, key2, MASK2)
self.lfsr3 = LFSR(128, key3, MASK3)
self.lfsr4 = LFSRSymbolic(128, key[-256:-128], MASK4)
def filter_polynomial(self, x0, x1, x2, x3):
# x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x3 + x1 + x2
return x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x3 + x1 + x2
def bit(self):
x,y,z,w = self.get_xyzw()
return self.filter_polynomial(x, y, z, w)
def get_xyzw(self):
x = self.lfsr1() + self.lfsr1() + self.lfsr1()
y = self.lfsr2()
z = (self.lfsr3() + self.lfsr3() + self.lfsr3() + self.lfsr3()) % 2
w = self.lfsr4() + self.lfsr4()
return x,y,z,w
def get_yz(self):
y = self.lfsr2()
z = self.lfsr3() + self.lfsr3() + self.lfsr3() + self.lfsr3()
return y,z
def stream(self, n):
return [self.bit() for _ in tqdm(range(n))]
def xor(self, a, b):
return [x + y for x, y in zip(a, b)]
def encrypt(self, pt: bytes):
pt_bits = [int(b) for b in bin(int.from_bytes(pt, 'big'))[2:].zfill(8 * len(pt))]
key_stream = self.stream(8 * len(pt))
return self.xor(pt_bits, key_stream)
def all_monomials(x1s, x2s):
d1_monos = x1s[:] + x2s[:]
d2_monos = []
for xi in x1s:
for xj in x2s:
d2_monos.append(xi*xj)
return [1] + d1_monos + d2_monos
def fast_coef_mat(monos, polys, br_ring):
mono_to_index = {}
for i, mono in enumerate(monos):
mono_to_index[br_ring(mono)] = i
# mat = matrix(GF(2), len(polys), len(monos))
mat = [[0] * len(monos) for i in range(len(polys))]
for i, f in tqdm(list(enumerate(polys))):
for mono in f:
# mat[i,mono_to_index[mono]] = 1
mat[i][mono_to_index[mono]] = 1
return mat
# x1[0] = 0, x2[0] = 0, x2[1] = 1
sol = (1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0)
x1 = [0] + list(sol[:127])
x2 = [0,1] + list(sol[127 : 127 + 126])
key1 = int(''.join(map(str, x1)), 2)
key2 = int(''.join(map(str, x2)), 2)
br256 = BooleanPolynomialRing(256, [f"x{i}" for i in range(256)])
key_sym = list(br256.gens())
cipher_sym = CipherSymbolicHalf(key_sym, key1, key2)
ct_bits = [int(b) for b in bin(int.from_bytes(ct, 'big'))[2:].zfill(8 * len(ct))]
# print(ct_bits.count(1))
out_list = cipher_sym.stream(len(pt) * 8)
eqs = []
for i, bit in tqdm(enumerate(ct_bits)):
eqs.append(out_list[i] - ct_bits[i])
x0s = key_sym[0:128]
x3s = key_sym[128:256]
monos = all_monomials(list(x0s), list(x3s))
print(f"[+] total equations {len(eqs)}")
print(f"[+] total monomials {len(monos)}")
mat = fast_coef_mat(monos, eqs, br256)
mat = matrix(GF(2), mat)
B = vector(GF(2),[mat[j,0] for j in range(len(eqs))])
mat = mat[:, 1:]
sol = mat.solve_right(B)
print(f"[+] solution found {sol}")
ZKPOF
I will use zero-knowledge proof to prove the knowledge for the factorization of n=p*q, so you wouldn’t be able to learn anything from it. Attachment
Writeup
The challenge implements a zero-knowledge proof of factoring:
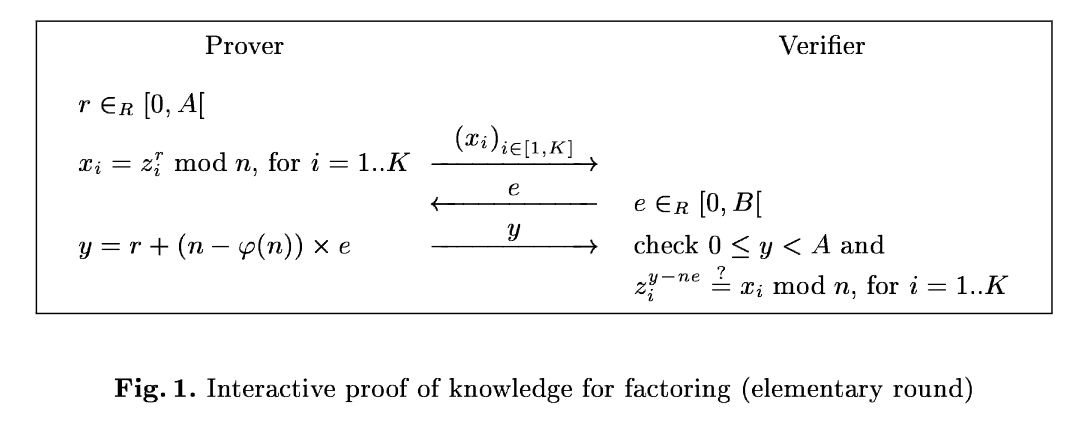
The key observation pertains not to cryptographic stuff but to the characteristics of Python. I spent the whole day analyzing the security parameters and finally gave up.
At the first glance, we can find a crucial flaw in source code: the protocol only checks $e \le B$. We can input negative $e$ to leak more information of $r$. However, the verifying process in the server do checks $0 \le y < A$ and we cannot recover $r$ by modulo $e$.
Right here, we can do binary search of $n - \varphi(n)$ using the check $y \ge 0$. Notice that $r$ is very close to $A$, the closer our guess is to $n - \varphi(n)$, the more precarious this comparison becomes (at most 10 bits can be recovered). Again, I failed to recover enough bits of $n - \varphi(n)$. Everything is stuck here and ultimately, I have resolved to implement a timely stop-loss.
Python Int Limit
As is known to all, the int type of python is unlimited. The limit in the sub-title does not mean storage size in memory for int, but the maximum length for the conversion between digit strings and int.
- If the length of digit string is more than 4300, you cannot convert it to
intdirectly. - If the value of
intis more than $10^{4300}$, you cannot convert it to string directly.
B = 10**4300
print(B)
# or
# B = int("1"*4300)
The above codes will throw an error:
ValueError: Exceeds the limit (4300 digits) for integer string conversion; use sys.set_int_max_str_digits() to increase
How can the integer-string converting exception be triggered in this challenge?
The useful triggers are rather subtle. We want to do binary search of $n - \varphi(n)$ using the check $y \le -10^{4300}$ which is stable during the whole search! Both json.loads and json.dumps include implicit integer string conversion and can be exploited in this challenge.
We can recover approximately $0x137$ msbs of $n - \varphi(n) = p + q - 1$ and then $0x137$ msbs of $p$ by:
\[(p-q) = (p + q)^2 - 4n \\ p = [(p + q) + (p -q)] // 2\]Finally, apply coppersmith to factor $n$.
Exploit
Exploit
from pwn import remote, process, log
import gmpy2
from Crypto.Util.number import getPrime, getRandomRange, GCD
from sage.all import PolynomialRing, Zmod
import json
import random
local = True
A = 2**1000
B = 2**80
if local:
io = process(["python3", "server.py"])
else:
io = remote("localhost", 1337)
n = int(io.recvline().decode().strip().split(" = ")[1])
def zkpof_verifier(io: remote, e: int):
io.sendlineafter(b"e = ", str(e).encode())
return io.recvline().decode()
def zkpof_prover(io:remote, n, z, phi):
r = getRandomRange(0, A)
x = pow(z, r, n)
io.sendlineafter(b"x = ", str(x).encode())
io.recvuntil(b"e = ")
e = int(io.recvline().decode().strip())
y = r + (n - phi) * e
io.sendlineafter(b"y = ", str(y).encode())
# let c = n - phi = p + q - 1
# y = r + c * e
lb = 1
ub = 2**513
bound_y = 10**4300
rand = random.Random(1337)
for i in range(0x137):
z = rand.randrange(2, n)
mid = (lb + ub) // 2
estimated_e = -bound_y // mid
response = zkpof_verifier(io, estimated_e)
if "Exceeds" in response:
# c*estimated_e > bound_y > mid * estimated_e
# c > mid
lb = mid
else:
ub = mid
log.info(f"lb = {lb}")
log.info(f"ub = {ub}")
# we have approximately 0x137 bits of p+q - 1 i.e. 0x137 bits of p+q
p_plus_q = (lb + ub) // 2
p_minus_q = int(gmpy2.isqrt(abs(p_plus_q**2 - 4 * n)))
p_h = (p_plus_q + p_minus_q) // 2
poly_ring = PolynomialRing(Zmod(n), 'x')
x = poly_ring.gen()
f = p_h + x
x0 = int(f.small_roots(beta=0.495, X=2**(512 - 0x137 + 3), epsilon=0.02)[0])
p = GCD(p_h + x0, n)
q = n // p
assert p * q == n
log.info("Successfully factored n")
phi = (p - 1) * (q - 1)
for i in range(13):
z = rand.randrange(2, n)
zkpof_prover(io, n, z, phi)
io.recvline().decode()
log.info(io.recvline().decode())
MatProd
A zero-day challenge for a crypto paper?! Attachment
Mat Prod Cryptosystem
In this challenge, we need to break two encryption systems claiming a security level of 128 bits in paper: New Public-Key Cryptosystem Blueprints Using Matrix Products in $F_p$.
Some notations ( matrix $D \le \alpha \iff \forall i,j \quad D_{ij} \le \alpha$)
- Dwarves $\mathfrak{D}$: Matrix $D$ over $\mathbb{F}_p$ with elements sampled from a set of small values i.e. $D \le \alpha$.
- Elves $\mathfrak{E}$: Matrix $E$ over $\mathbb{F}_p$ with elements sampled as normal value i.e. $E \le p$.
Direct Matrix Product Cryptosystem
Let secret matrix set $\mathbf{A} \subset \mathfrak{D}$ . Trapdoor for the direct construction. Let $D \in \mathfrak{D}$ and $E \in \mathfrak{E}$ be two secrets. For each $A_i \in \mathbf{A}$, let $\overline{A_i}:=E A_i Y$, where $Y:=D E^{-1}$ is also secret. Encrypt some permutation $\sigma$ :
\[\sigma \overline{\mathbf{A}}=\prod_{i=0}^{k-1} \bar{A}_{\sigma(i)}=\prod_{i=0}^{k-1} E A_{\sigma(i)} Y=E\left(\prod_{i=0}^{k-1} A_{\sigma(i)} D\right) E^{-1}\]Alternating Matrix Product Cryptosystem
Let public matrix sets $\mathbf{A^0}, \mathbf{A^1} \subset \mathfrak{D}$. Let $E_0, \ldots, E_k$ be secret distinct elves. For each $A_{i}^{b} \in \mathbf{A^b}$ compute $\bar{A_i}^{b} = E_{i} A_{i}^{b} E_{i+1}^{-1} $ as public key. Encrypt message bits $m$ :
\[m \overline{\mathbf{A}}=\prod_{i=0}^{k-1} \bar{A}_i^{m_i}=\prod_{i=0}^{k-1} E_i A_i^{m_i} {E_{i+1}^{-1}}=E_0(m \mathbf{A}) E_k^{-1}\]Break Direct Cryptosystem
I solved this part during the competition. Given private key $D \in \mathfrak{D}$ and $E \in \mathfrak{E}$, we can recover $M =\prod_{i=0}^{k-1} A_{\sigma(i)} D$. Since $A_i, D_i \le \alpha \ll p$, if we multiply by the correct guess of $\bar A_{\sigma(0)}^{-1}$ in the left, the result matrix $M_0 = \bar A_{\sigma(0)}^{-1} M = \prod_{i=1}^{k-1} A_{\sigma(i)} D$ will be smaller than $M$ and thus we can recover the original permutation $\sigma$ sequentially.
Given the ciphertext $C = \sigma \overline{\mathbf{A}}$ and public key $\bar{\mathbf{A}^{0}}, \bar{\mathbf{A}^{1}} \subset \mathfrak{D}$, can we distinguish $\bar A_{\sigma(0)}^{-1} C$ from all other choices: $\bar A_{\sigma(i)}^{-1} C, i\ne 0$ without the secret keys $D, E, \mathbf{A}$?
To address this, we need to identify a pertinent matrix property that distinguishes between the aforementioned scenarios. Let’s deep dive into the trace of matrix.
Definition: The trace of a square matrix is the sum of its diagonal elements:
\[tr(A) = \sum_{i=1}^{n} A_{ii}\]
The trace of $M =\prod_{i=0}^{k-1} A_{\sigma(i)} D$ is relatively small compared to $p$ and $C = EME^{-1}$. Let’s consider the basic identity of trace : $tr(AB) = tr(BA)$ because the diagonal elements of $AB$ and $BA$ are the same. By associative property of matrix multiplication:
\[tr(ABC) = tr(CAB) = tr(BCA)\]Then for the ciphertext:
\[tr(C) = tr(EME^{-1}) = tr(E^{-1}EM) = tr(M)\]The identity actually means the trace is an invariant of similar matrices. If the trace of $M$ does not exceed $p$, multiplying the correct $\bar A_{\sigma(0)}^{-1}$ in the left of $C$ will decrease the trace while multiplying the incorrect ones won’t i.e.
\[\begin{aligned} tr(\bar A_{\sigma(0)}^{-1} C) &= tr(E\prod_{i=1}^{k-1} A_{\sigma(i)} D E^{-1}) \\ &= tr(\prod_{i=1}^{k-1} A_{\sigma(i)} D) \\ & \le tr(\prod_{i=0}^{k-1} A_{\sigma(i)} D) = tr(C) \end{aligned}\]By DFS search, we can recover the original permutation and then the decoded plaintext.
Break Alternating Cryptosystem
I did not solve this part. This section primarily references maple’s writeup.
In alternating cryptosystem, the ciphertext of message bits $m$ is :
\[\begin{aligned} C &= m \overline{\mathbf{A}} = \prod_{i=0}^{k-1} \bar{A}_i^{m_i} \\ &=\prod_{i=0}^{k-1} E_i A_i^{m_i} {E_{i+1}^{-1}} \\ &=E_0(m \mathbf{A}) E_k^{-1} \end{aligned}\]Now the kernel $m \mathbf{A} = A_i^{m_i} $ is small and thus $tr(m \mathbf{A})$ is small. But in this case the ciphertext $C$ is no longer similar to the kernel $m \mathbf{A}$.
In this section, we need one more identity of trace which is:
\[tr(AB) = \mathsf{flatten}(A) \mathsf{flatten}(B)^T\]where $A, B$ is $n \times n$ matrix and flatten is a trivial flatten mapping: $\mathbb{F}^{n \times m} \mapsto \mathbb{F}^{1 \times nm}$ equivalent to vector(mat.list()) in sage. The identity is easy to prove by the definition of trace, omitted here.
Therefore, the trace of ciphertext $C$ is:
\[\begin{aligned} tr(C) &= tr(E_0(m \mathbf{A}) E_k^{-1}) \\ &= tr(E_k^{-1} E_0 (m \mathbf{A})) \end{aligned}\]The identity does not fully leverage the ciphertext information, but can be transformed into a variant of the hidden subset-sum problem. I don’t know if it is solvable using orthogonal lattice in this challenge. To fully leverage $C$, we consider the unknown trace of $mA$:
\[\begin{aligned} tr(mA) &= tr(E_{0}^{-1} C E_k) \\ &= tr(E_kE_0^{-1} C) \end{aligned}\]In the flattened perspective,
\[\begin{aligned} tr(mA) &= \underbrace{\mathsf{flatten}(E_kE_0^{-1})}_{E_{k,0} \in F_p^{1\times n^2}} \underbrace{\mathsf{flatten}(C)}_{Y_m \in F_p^{1\times n^2}}{}^T \\ &= E_{k, 0} Y_m^T \end{aligned}\]We can use the public key to generate as many ciphertexts as we want i.e. $C_1 = E(m_1), \cdots, C_{t} = E(m_k)$.
\[\begin{aligned} tr(m_1 \mathbf{A}) &= E_{k, 0} Y_{m_1}^T \\ tr(m_2 \mathbf{A}) &= E_{k,0} Y_{m_2}^T \\ & \cdots \\ tr(m_t \mathbf{A}) &= E_{k, 0} Y_{m_t}^T \end{aligned}\]where $E_{k, 0}$ is fixed and $Y_{m_1}, \cdots, Y_{m_t}$ are known $n^2$-dimension vectors. By choosing some $t$, we can recover $E_{k, 0}$ but it is still not clear how to recover the secret bits. The core question is still:
How can we distinguish $\bar{A_0^1} ^{-1} C$ from $\bar{A_0^0} ^{-1} C$ if the first bit of message $m$ is 1?
Observe that we can also generate partial ciphertexts i.e. prod of the last $n-1$ matrix randomly chosen from $\mathbf{A^0}, \mathbf{A^1}$. Let $m_1, \cdots, m_t$ be $(n-1)$-bit string and $Y_{m_1}, \cdots, Y_{m_t}$ are the flattened vector of $C_{m_1}, \cdots C_{m_t}$ :
\[\begin{aligned} tr(m_1 \mathbf{A}) &= E_{k, 1} Y_{m_1}^T \\ tr(m_2 \mathbf{A}) &= E_{k, 1} Y_{m_2}^T \\ & \cdots \\ tr(m_t \mathbf{A}) &= E_{k, 1} Y_{m_t}^T \end{aligned}\]Denote matrix $M$ as:
\[M = \begin{bmatrix} Y_{m1}^T & Y_{m_2}^T & \cdots & Y_{m_t}^T \end{bmatrix}_{n^2 \times t}\]Assuming $tr(m_i \mathbf{A}) \ll p$ , then the lattice $M$ modulo $p$ contains small vector $t$ which can be represented as:
\[t = (tr(m_1 \mathbf{A}), tr(m_2 \mathbf{A}), \cdots, tr(m_t \mathbf{A}))\]LLL the lattice $M$ modulo $p$ to recover $t$ and then solve $x$ for $xM = t \mod p$ where $x$ is (quasi-)equivalent to $E_{k,1}$. Up to this point, we can utilize $E_{k,1}$ to distinguish the rationality of certain partial ciphertext.
- Case 1: if a ciphertext is valid partial ciphertext $C^{\prime} = \prod_{i=1}^{k-1} {\bar{A_i}^{m_i}} = {E_1} (m^{\prime} \mathbf{A}) {E_k^{-1}}$ encrypting $k-1$ bits. Then the trace $tr(m^{\prime} \mathbf{A}) = E_{k, 1} \mathsf{flatten(C^\prime)}^T$ is small.
- Case 2: if a ciphertext $C^\prime$ is not valid partial ciphertext i.e. decrypting the first bit with wrong matrix, $ E_{k, 1} \mathsf{flatten(C^\prime)}^T$ will be a random value in $\mathbb{F}_{p}$, around $\frac{p}{2}$.
Finally, we can decrypt message bits sequentially by finding all the distinguishing matrix:$E_{k,i} = E_{k} E_{i}^{-1}$.
Remarks
In this challenge, the condition $tr(m_i \mathbf{A}) \ll p$ holds true. To reduce the time of lattice reduction, we can use two methods to optimize:
-
Bruteforcing: $a$ bits for one $E_{k,j}$ instead of one bit for one $E_{k,j}$. For the first time we skip the first $a$ bits, and try to find $E_{k,a}$. Then brute force the first $a$ bits to find a valid partial ciphertext using $E_{k,a}$. Continue this process until the last $a$ bits. In the last step, only brute forcing is needed since there are no partial ciphertexts to be found.
-
Lattice Reduction with Modulo: this is what I learned from maple’s codes. Typically, for a $n \times t$ matrix $M$, we would construct
\[L = \begin{bmatrix} M \\ pI \\ \end{bmatrix}_{(n+t) \times (t)}\]to do lattice reduction modulo $p$. If $t > n$, the reduction can be optimized to dimension $(t, t)$. We first do gaussian elimination on $L$ to get a well-formatted matrix:
\[M_e = \begin{bmatrix} I_{n \times n} & E_{n \times (t-n)} \end{bmatrix}_{n \times t}\]Then build a $t \times t$ matrix:
\[L_o = \begin{bmatrix} I_{n \times n} & E_{n \times (t-n)} \\ 0_{(t-n) \times n} & p \cdot I_{(t-n) \times (t-n)} \end{bmatrix}_{n \times t}\]Doing LLL reduction on $L_o$ is somewhat equivalent to doing LLL reduction on $M$ modulo $p$.
Implementation
Implementations of the above two attacks with detailed comments: Attacks.